Computational Fluid Dynamics Development
On the Earth, 2/3 of the matter is fluid such as the air in the atmosphere, the water in the sea, or even the blood in our human bodies. Most of the fluids flow in the state of turbulence, which means that the flow parameters such as velocity, pressure, density, etc are always randomly fluctuating with time. The turbulence will increase the friction drag of an airplane, the heat transfer of air conditioning, and enahnce the mixing between two fluids such as coffee and cream. For high speed aerodynamic flows, there is also a phenomenon called shock wave, which is an extremely thin surface. Across a shock wave, the flow parameters such as pressure, temperature, velocity jump. Such a jump is a discontinuity in the mathematics sense. The other example of discontinuity is the contact surface between air and water, across which the density jumps about 1000 times. Even though the density has a jump, the velocity and pressure at the contact surface are the same such as the ocean wave driven by the wind of hurricane.
The governing equations of fluid motion are the Navier-Stokes equations, which are based on mass conservation, Newton's 2nd law, and energy conservation. The Navier-Stokes equations are hence composed of partial differential derivatives in time and space. We all know that a derivative does not exist across a discontinuity.
How to calculate the turbulent flow fields with shock waves or contact discontinuities is a very challenging and unsolved problem. One of our research interests is to simulate these turbulent flow fields using large eddy simulation (LES) and detached eddy simulation (DES). We have developed high order (5th and 7th order) finite difference weighted essentially non-oscillatory (WENO) schemes to capture the shock waves and contact discontinuities. We also developed a fully conservative 4th and 6th order central differencing schemes for the viscous terms in Navier-Stokes equations. In mathematics term, a numerical scheme that can resolve the discontinuities is called Riemann solver. In our research, a E-CUSP upwind scheme is developed and it can capture crisp shock profiles and exact contact surfaces. The E-CUSP scheme is used with those high order WENO schemes for turbulence simulation and fluid-structural interactions. An implicit Gauss-Seidel line relaxation with 2nd order temporal accuracy is used to avoid the approximate factorization errors (such as those in Beam-Warming scheme, Jameson's LU-SGS scheme) and achieve high convergence rate.
We have also developed the Non-Reflective boundary conditions for 3D unsteady Navier-Stokes equations to avoid wave reflections at the computational boundaries, which can contaminate the flow solutions and distort the simulated results. A general sub-domain boundary mapping procedure is created in our research for parallel computation of the flow fields. The parallel computation is to partition a large domain to multiple smaller sub-domains and conduct the calculation simultaneously on multiple processors to save wall clock time. We have built a Beowulf Linux cluster system in our CFD lab for parallel computing.
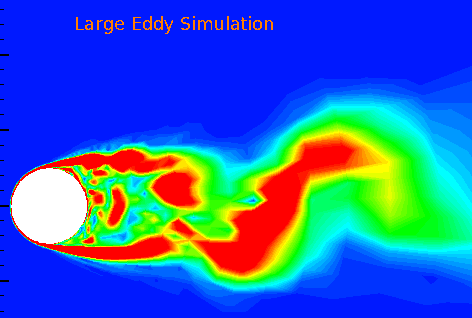
The following is a LES result animation of the vorticity field in a 3D turbulent flow passing a cylinder at Reynolds number of 3900 and incoming Mach number of 0.2.
Recent Publications:
Journal:
- Chen, X. and Zha, G.-C., "Implicit Application of Non-Reflective Boundary Conditions for Navier-Stokes Equations in Generalized Coordinates ", International Journal for Numerical Methods in Fluids, Vol. 50, No. 7, pp767-793, 2006
- Zha, G.-C., "A Low Diffusion Efficient Upwind Scheme " , AIAA Journal, Vol.43, No.5, pp 1137-1140, 2005
- Hu, Z. and Zha, G.-C.,"Calculations of 3D Compressible Using an Efficient Low Diffusion Upwind Scheme",International Journal for Numerical Methods in Fluids, Vol. 47, pp253-269, Nov. 2004
- Zha, G.-C.,"Boundary Layer Loss Mechanism and Justification of Wall Functions for Turbulence Modeling" , AIAA Journal, Vol. 42, No. 11, Nov. 2004, p2387-2390
- Zha, G.-C. and Hu, Z.,"Calculation of Transonic Internal Flows Using an Efficient High Resolution Upwind Scheme" , AIAA Journal, Jan. 2004
- Zha, G.-C, "Numerical Tests of Upwind Scheme Performance for Entropy Condition", AIAA Journal, Vol. 37, No. 8, August 1999, p. 1005-1007
CONFERENCE(downloadable)
- Baoyuan Wang, Bahaa Haddoukessouni, Jonathan Levy and G.-C. Zha, "Numerical Investigations of Injection Slot Size Effect on the Performance of Co-Flow Jet Airfoil",AIAA Paper 2007-4427 25th AIAA Applied Aerodynamics Conference, June 25-28, 2007
- Baoyuan Wang and G.-C. Zha, "A GENERAL SUB-DOMAIN BOUNDARY MAPPING PROCEDURE FOR STRUCTURED GRID CFD PARALLEL COMPUTATION",AIAA Paper 2007-4432 25th AIAA Applied Aerodynamics Conference, June 25-28, 2007
- Yiqing Shen, Baoyuan Wang and G. Zha, "Comparison Study of Implicit Gauss-Seidel Line Iteration Method for Transonic Flows",AIAA Paper 2007-4332 18th AIAA Computational Fluid Dynamics Conference, June 25-28, 2007
- Yiqing Shen, Baoyuan Wang and G. Zha, "Implicit WENO Scheme and High Order Viscous Formulas for Compressible Flows",AIAA Paper 2007-4431 25th AIAA Applied Aerodynamics Conference, June 25-28, 2007
- Hu, Z. and Zha, G.-C. "Parallel Computation of Forced Vibration for A Compressor Cascade ", AIAA Paper 2006-0628, AIAA the 44th Aerospace Sciences Meeting and Exhibit Conference, Jan. 8-12, 200\6, Reno, NV
- Chen, X. and Zha, G.-C., "Implicit Application of Non-Reflective Boundary Conditions for Navier-Stokes Equations in Generalized Coordinates ", AIAA Paper 2005-0091, AIAA the 43rd Aerospace Sciences Meeting and Exhibit Conference, Jan. 10-13, 2005, Reno, NV
- Zha, G.-C., "A Low Diffusion E-CUSP Upwind Scheme for Transonic Flows " , AIAA Paper 2004-2707, 34th AIAA Fluid Dynamics Conference and Exhibit, 28 Jun - 1 Jul 2004, Portland, Oregon
- Hu, Z. and Zha, G.-C.,"Numerical Study of a Casacde Unsteady Separated Flow" , ASME Paper GT2004_53195, ASME TURBO EXPO 2004, June 14-17, 2004, Vienna, Austria
- Zha, G.-C.,"Boundary Layer Loss Mechanism and Justification of Wall Functions for Turbulence Modeling" , AIAA-2004-1118, AIAA the 42st Aerospace Sciences Meeting and Exhibit Conference, Jan. 5-8, 2004, Reno, NV
- Zha, G.-C. and Hu, Z., "Calculation of Transonic Internal Flows Using an Efficient High Resolution Upwind Scheme" , AIAA-2004-1097, AIAA the 42st Aerospace Sciences Meeting and Exhibit Conference, Jan. 5-8, 2004, Reno, NV
- Zha, G.-C. and Hu, Z.,"Numerical Study on Flow Separation of A Transonic Cascade" , AIAA-2004-0199, AIAA the 42st Aerospace Sciences Meeting and Exhibit Conference, Jan. 5-8, 2004, Reno, NV
- Zha, G-C. And Chakradhar, L., "On the Accuracy of Runge-Kutta Method for Linear Wave Equation", AIAA-2003-0248, AIAA the 41st Aerospace Sciences Meeting and Exhibit Conference, Jan. 6-9, 2003, Reno, NV
- Zha, G.-C , "Comparative Study of Upwind Scheme Performance for Entropy Condition and Discontinuities," AIAA Paper 99-3348, the 14th AIAA Computational Fluid Dynamics Conference, June 28 - July 1, 1999,
